
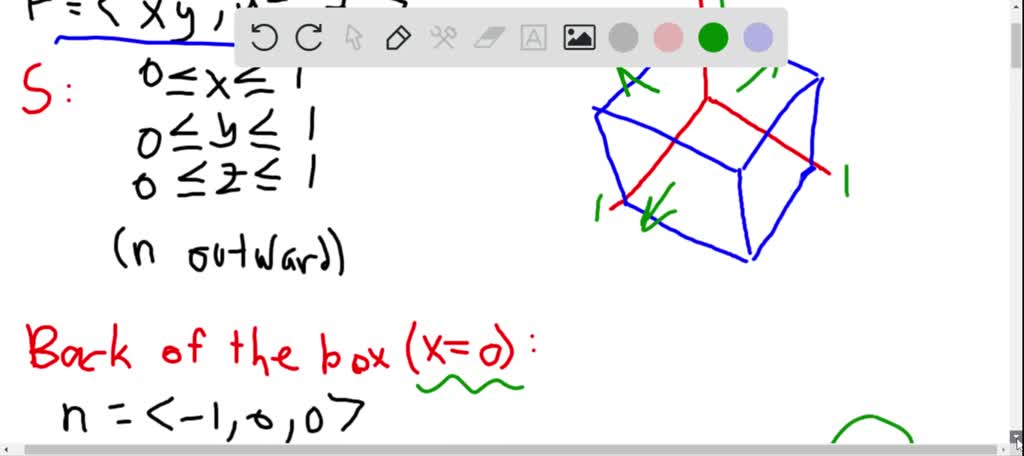
The light turns green, and you start driving at 30mph down the road. You're sitting at a stoplight, and the wipers are at just the right speed to keep the windshield clean. Suppose there's a nice spring shower outside and you're out driving a car. Tip: to type the character Φ in Mathematica, type the following keys in order: Esc, P, h, i, Esc. Every time you do a surface integral of a vector field, you should make sure you're using a normal vector that points in the correct direction (which should be specified in the problem). The integral represents the flux from the "inside" of the surface to the "outside" - the direction in which the normal vector points is considered "outside". It's important to get the orientation of the surface right. Similarly, if F is moving perpendicular to the surface, || F|||| n|| will be multiplied by cos 0 = 1, so F has as much effect as it can.
The cosine takes care of the ``tilt'': if the vector field is moving in the same direction as the surface, it isn't pushing any particles at all through the surface in that case, cos θ = cos (π/2) = 0 (remember that the normal vector will be perpendicular to F in this case). In this case, we see that the length of the normal vector is the area of the spanned parallelogram, which is multiplied by the length of F at that point.

n represents the scalar triple product of the partial derivatives and F, which we know is equal to the volume of the parallelepiped spanned by those vectors (up to a possible minus sign).Īnother way to see this is to rewrite the dot product: F.There are at least two ways to convince yourself that this definition makes sense. Remember, the dot product of two vectors is a number, so our final integrand will actually still be a scalar function. In this case we'll take the dot product of our vector field with the normal vector. For scalar functions we multiplied the scalar function by the length of the normal vector. This definition is very similar to the one for surface integrals of scalar functions, which you can find in your textbook. This is equal to -( × ), so the only difference in your final answer is a negative sign.) (Note that, depending on which way the normal vector is supposed to point, you might use ( × ) instead. The surface integral (or flux integral) of F over M is: Let F: U⊂ → be a continuous vector field, and let M be a smooth surface lying in U that is parametrized by Φ(u,v), where (u,v) ⊂ R ε. Just for your reference, we'll repeat the definition of a surface integral of a vector field.

The precise definition of a surface integral (or flux integral the two terms are interchangeable) of a vector field is in the next section. We interpret the result as "amount of fluid (or particles) moving across the surface per unit time". To find the volume of that parallelepiped, we use the scalar triple product: we take the cross product of the sides of the parallelogram, and then find the dot product of that with the vector from the vector field. There's a picture and some more descriptions of this in your text. In that case, the sides of the parallelogram and the vector representing the vector field form a parallelepiped.

Consider a very small bit of the surface (a small parallelogram, for example), so small that we can consider the vector field to be constant over that parallelogram. Say the vector field represents velocity. Let's make that a little bit more precise. Instead, the question we'll want to answer is: how much is the vector field pushing particles across the surface? What about surface integrals? That is, what about integrating a vector field over some parametrized surface in three-dimensional space?įor surfaces, it no longer makes much sense to ask how much the vector field is pushing particles along the surface. Robin:"But that's only for half a minute!"īatman:"That's all we'll need, if my calculus is correct."īy now you're familiar with line integrals of vector fields, which in a certain sense measure how much the vector field is "pushing particles" along the path - over a closed path, we called that circulation. Questions to: or an eclipse of the sun due." Lab 6B - Surface Integrals of Vector Fields


 0 kommentar(er)
0 kommentar(er)
